近年来,为应对日益严峻的大范围、持续性严重雾霾污染,我国借鉴欧洲、美国等发达国家经验,在全国范围内开展区域联防联控(JPCAP)已成为我国区域性大气污染治理的重要战略举措。自2013年10月京津冀及周边地区大气污染防治协作机制正式启动以来,长三角区域、山东省省会城市群、昌九区域等区域紧随其后纷纷启动大气污染防治协作机制,但各区域联防联控实际进展缓慢,区域空气质量改善效果并不明显。造成这种局面的原因很多,其中联防联控区域范围界定不科学是重要原因之一。一个区域的空气质量同时受社会经济发展(经济发展水平、能源与产业结构、技术水平、人口规模等)和自然环境(地形地貌、风速风向、温度、湿度等) 等因素影响,并随时间变化而动态变化。因此,如何全面考虑这些因素、科学界定JPCAP区域范围成为促进JPCAP实施进程并提高其有效性的关键。而近年来污染监测网络日益完善、获得长期海量监测数据成为现实,为本研究提供了新的契机。鉴于此,本文提出了综合运用相关性分析、回归分析、聚类分析等数据挖掘技术进行大气污染联防联控区域划分的新方法,并应用到中国长三角区域15个城市的细颗粒物(PM2.5)和臭氧(O3)污染联防联控的实证案例。
一、研究方法
针对一个包含m个城市的大区域R的某种大气污染p,本研究采用线性回归分析、相关性分析和聚类分析等数据挖掘技术对m个城市的海量长期污染监测数据进行深入挖掘。以城市为基本划分单元,将R划分为若干联防联控子区域,具体步骤如下:
Step 1:采用一元线性回归分析识别各城市对R区域的污染影响程度,将污染贡献较大的城市作为参与联控区域划分的候选城市。以某城市的污染物p的日均浓度(Xp)为自变量,以R区域的污染物p的日均浓度(Yp)为因变量进行一元线性回归,回归方程Yp=a·Xp+ b的斜率a越大,表明该城市的污染浓度变化对区域R第p种污染物的影响越大。给定一个判别临界值a0,当回归方程的斜率a> a0时,对应的城市即可作为联防联控区域划分的候选城市。
Step 2:对候选城市的长期污染数据进行相关性分析,求得城市间污染相关系数矩阵M。基于长期污染监测数据,计算任意两城市x与y的皮尔逊相关系数r(如式1),r值越接近于1,说明两城市之间的污染相关性越高,意味着它们彼此间的污染传输水平越高,或它们在污染排放特征方面存在较高的一致性。
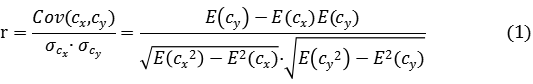
其中,cx与cy分别代表城市x、y的污染物浓度,Cov(cx, cy)为x、y污染浓度的协方差,σ为标准差,E(·)代表数学期望。
Step 3:以城市为变量,以相关系数矩阵M中的r为观察值,对候选城市进行聚类分析,聚类后得到的类(Clusters)即为区域R的联防联控子区域。
二、实证研究结果
长三角区域冬春季易爆发严重雾霾污染,夏秋季常爆发严重的臭氧污染,是我国推行重点区域联防联控的区域之一。本研究以长三角区域15个城市为研究单元,包括上海(SH)、浙江省的杭州(HAZ)、湖州(HUZ)、嘉兴(JX)、绍兴(SX)、宁波(NB)、台州(TZZ)和江苏省的南京(NJ)、苏州(SZ)、无锡(WX)、常州(CZ)、扬州(YZ)、镇江(ZJ)、泰州(TZJ)、南通(NT),他们都有着密集的人口、发达的经济、交通、建筑业等,如图1所示。
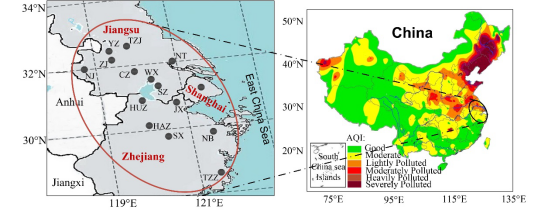
图1 长三角区域15市的污染水平及地理分布图
表1展示了15市PM2.5和O3对整个区域的贡献水平的回归分析结果。显然,各城市PM2.5对应的斜率均不低于0.724,说明各城市污染浓度变化对整个区域影响很大,因此可将15市全部纳入联防联控候选城市群。对于O3,所有回归方程的斜率均介于0.428和0.537之间,说明各城市O3浓度变化对整个区域O3污染水平的影响程度较弱。为了识别哪些城市可能会被划分在一起从而组成一个新的小范围的O3联动区域,仍然将15个城市均作为O3联动候选城市。
表1 长三角区域与各城市污染浓度的线性回归结果
|
城市
|
线性回归方程
|
R2
|
P
|
PM2.5
|
SH
|
Y=14.290+0.757 X
|
0.785
|
<0.001
|
HUZ
|
Y= 8.133+0.861 X
|
0.834
|
<0.001
|
HAZ
|
Y= 9.772+0.828 X
|
0.724
|
<0.001
|
JX
|
Y=5.937+0.924 X
|
0.885
|
<0.001
|
SX
|
Y=9.827+0.821 X
|
0.718
|
<0.001
|
NB
|
Y=16.166+0.866 X
|
0.755
|
<0.001
|
TZZ
|
Y=21.020+0.808 X
|
0.458
|
<0.001
|
SZ
|
Y=6.566+0.830 X
|
0.914
|
<0.001
|
NJ
|
Y=13.189+0.734 X
|
0.832
|
<0.001
|
WX
|
Y=4.579+0.824 X
|
0.937
|
<0.001
|
YZ
|
Y=9.292+0.832 X
|
0.788
|
<0.001
|
CZ
|
Y= 11.095+0.740 X
|
0.928
|
<0.001
|
ZJ
|
Y=8.570+0.780 X
|
0.841
|
<0.001
|
NT
|
Y=12.991+0.739 X
|
0.818
|
<0.001
|
TZJ
|
Y= 10.928+0.724 X
|
0.796
|
<0.001
|
O3
|
SH
|
Y= 11.211+0.504 X
|
0.760
|
<0.001
|
HUZ
|
Y= 17.558+0.428 X
|
0.790
|
<0.001
|
HAZ
|
Y= 19.582+0.475 X
|
0.761
|
<0.001
|
JX
|
Y= 13.949+0.458 X
|
0.787
|
<0.001
|
SX
|
Y= 25.946+0.437 X
|
0.688
|
<0.001
|
NB
|
Y= 10.970+0.537 X
|
0.701
|
<0.001
|
TZZ
|
Y= 14.984+0.509 X
|
0.557
|
<0.001
|
SZ
|
Y= 14.983+0.506 X
|
0.848
|
<0.001
|
NJ
|
Y= 18.838+0.448 X
|
0.773
|
<0.001
|
WX
|
Y= 16.084+0.484 X
|
0.825
|
<0.001
|
YZ
|
Y=11.387+0.489 X
|
0.740
|
<0.001
|
CZ
|
Y= 21.353+0.459 X
|
0.663
|
<0.001
|
ZJ
|
Y= 18.191+0.433 X
|
0.760
|
<0.001
|
NT
|
Y= 7.830+0.522 X
|
0.773
|
<0.001
|
TZJ
|
Y= 16.519+0.473 X
|
0.716
|
<0.001
|
表2为15市任意两个城市之间两种污染物的皮尔逊(Pearson)相关系数矩阵,对角线下方为PM2.5污染相关系数,对角线上方为O3污染相关系数。显然,无论是PM2.5还是O3,任意两个城市的污染相关系数均在0.01显著水平上通过检验。
表2 皮尔逊相关系数矩阵
|
SH
|
HUZ
|
HAZ
|
JX
|
SX
|
NB
|
TZZ
|
SZ
|
NJ
|
WX
|
YZ
|
CZ
|
ZJ
|
NT
|
TZJ
|
SH
|
1
|
0.79*
|
0.77*
|
0.90*
|
0.74*
|
0.83*
|
0.73*
|
0.88*
|
0.74*
|
0.84*
|
0.73*
|
0.71*
|
0.78*
|
0.89*
|
0.77*
|
HUZ
|
0.77*
|
1
|
0.91*
|
0.90*
|
0.83*
|
0.79*
|
0.70*
|
0.92*
|
0.86*
|
0.91*
|
0.81*
|
0.82*
|
0.82*
|
0.78*
|
0.80*
|
HAZ
|
0.63*
|
0.88*
|
1
|
0.90*
|
0.89*
|
0.85*
|
0.77*
|
0.88*
|
0.80*
|
0.85*
|
0.76*
|
0.79*
|
0.75*
|
0.73*
|
0.72*
|
JX
|
0.90*
|
0.88*
|
0.81*
|
1
|
0.82*
|
0.88*
|
0.77*
|
0.92*
|
0.79*
|
0.87*
|
0.76*
|
0.78*
|
0.77*
|
0.81*
|
0.75*
|
SX
|
0.68*
|
0.83*
|
0.93*
|
0.84*
|
1
|
0.79*
|
0.70*
|
0.81*
|
0.74*
|
0.79*
|
0.69*
|
0.65*
|
0.73*
|
0.71*
|
0.73*
|
NB
|
0.80*
|
0.81*
|
0.81*
|
0.88*
|
0.85*
|
1
|
0.86*
|
0.83*
|
0.70*
|
0.77*
|
0.68*
|
0.71*
|
0.69*
|
0.73*
|
0.66*
|
TZZ
|
0.56*
|
0.60*
|
0.69*
|
0.63*
|
0.67*
|
0.73*
|
1
|
0.71*
|
0.61*
|
0.68*
|
0.61*
|
0.61*
|
0.61*
|
0.65*
|
0.61*
|
SZ
|
0.93*
|
0.86*
|
0.75*
|
0.94*
|
0.76*
|
0.83*
|
0.62*
|
1
|
0.87*
|
0.96*
|
0.84*
|
0.85*
|
0.85*
|
0.87*
|
0.84*
|
NJ
|
0.71*
|
0.84*
|
0.79*
|
0.81*
|
0.74*
|
0.72*
|
0.55*
|
0.83*
|
1
|
0.89*
|
0.91*
|
0.81*
|
0.90*
|
0.80*
|
0.86*
|
WX
|
0.89*
|
0.89*
|
0.78*
|
0.93*
|
0.78*
|
0.82*
|
0.58*
|
0.97*
|
0.88*
|
1
|
0.88*
|
0.90*
|
0.89*
|
0.87*
|
0.86*
|
YZ
|
0.71*
|
0.76*
|
0.70*
|
0.75*
|
0.67*
|
0.65*
|
0.52*
|
0.80*
|
0.89*
|
0.82*
|
1
|
0.82*
|
0.89*
|
0.82*
|
0.90*
|
CZ
|
0.84*
|
0.86*
|
0.77*
|
0.88*
|
0.75*
|
0.79*
|
0.59*
|
0.93*
|
0.90*
|
0.96*
|
0.89*
|
1
|
.075*
|
0.74*
|
0.70*
|
ZJ
|
0.75*
|
0.79*
|
0.72*
|
0.80*
|
0.70*
|
0.68*
|
0.49*
|
0.83*
|
0.92*
|
0.88*
|
0.95*
|
0.91*
|
1
|
0.85*
|
0.90*
|
NT
|
0.92*
|
0.76*
|
0.62*
|
0.84*
|
0.64*
|
0.74*
|
0.55*
|
0.90*
|
0.76*
|
0.89*
|
0.80*
|
0.89*
|
0.83*
|
1
|
0.89*
|
TZJ
|
0.77*
|
0.74*
|
0.65*
|
0.76*
|
0.64*
|
0.65*
|
0.51*
|
0.83*
|
0.83*
|
0.85*
|
0.92*
|
0.90*
|
0.92*
|
0.89*
|
1
|
*. Correlation is significant at the 0.01 level (2-tailed).
对角线上方为“城市对”的O3相关系数,下方为PM2.5相关系数
|
图2(a)是对PM2.5联动候选城市的聚类树状图,15市被分成4组,每一组内城市间的污染相关性特征最相似,即每一组就是长三角区域的一个联动子区域。由此,长三角可划分为4个PM2.5联动子区域,分别为R1={苏州、无锡、常州、嘉兴、湖州、上海、南通}、R2={扬州、镇江、泰州、南京}、R3={杭州、绍兴、宁波}、R4={台州}。同理,长三角区域的15个O3联动候选城市可划分为9个O3联控子区域,分别为R1={苏州、无锡、湖州}、R2={杭州、嘉兴}、R3={上海}、R4={南通}、R5={南京、扬州、镇江、泰州}、R6={常州}、R7={绍兴}、R8={宁波}、R9={台州},如图2(b)所示。长三角区域的4个PM2.5联控子区域和9个O3联控子区域的地理分布示意图如图3所示。从联防联控范围划分结果易知,臭氧具有小范围局地污染特征,因此更适合在小范围内开展联防联控。
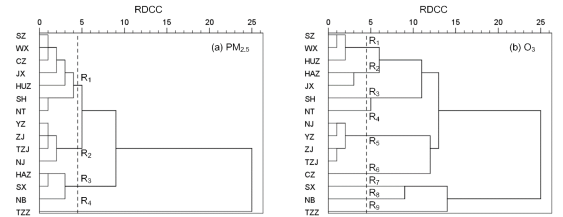
图2 长三角区域联动候选城市聚类树状图
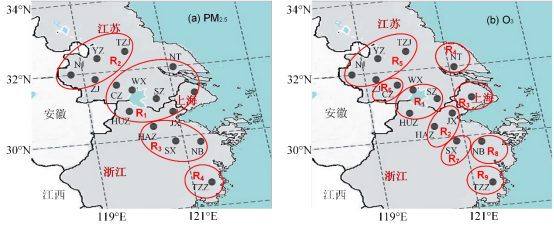
图3 长三角区域PM2.5与O3联控子区域划分
三、研究结论与对策建议
PM2.5自身的物化特性决定其在空气中易长时间悬浮并随风传输,适宜在较大的区域范围内开展联动治理。在长三角的4个PM2.5联动子区域中,R1={苏州、无锡、常州、嘉兴、湖州、上海、南通}和R2={扬州、镇江、泰州、南京}的范围均较大,R3={杭州、绍兴、宁波}和R4={台州}范围较小,这是由于R3和R4污染水平相对低,且均处于西北风向末端的临海位置,自然扩散条件较好,且受来自西北内陆“脏气团”污染输入的影响比较小。而R2处于长三角区域西北部,受西北内陆污染输入的影响较大,且在R2的经济发展中,石油、化工、黑色金属、有色金属等6大高污染行业扮演重要角色,扬州、镇江、泰州、南京应加强产业结构调整和优化,强化对高污染行业尤其是化工、石化等的污染治理。R1的6大高污染行业的石化、化工行业经济贡献远低于R2,而大气污染排放较小的计算机通信和电子设备业、纺织和服装业相对发达。
与PM2.5不同,长三角被细分为9个范围较小的O3联动子区域,除R1={苏州、无锡、湖州}和R5={南京、扬州、镇江、泰州}外,其它7个子区域所包含的城市均不超过2个,说明O3属于小范围局地污染。快速的工业化和区域一体化进程使长三角区域内各城市资源及生态环境具有共性特征,且各城市自然地理条件相仿、生态功能特征相似,大气环境问题相近,区域内一江、一湖、一海(即长江、太湖、东海)以及纵横交错的水网将苏浙沪生态环境牢牢地嵌套成为一个“唇齿相依”的整体,这些条件也极易使O3污染在各城市间呈现出“一荣俱荣、一损俱损”的共性特征。因此,对呈现小范围局地污染特征的O3污染治理,我们可将具有共同污染特征的城市作为一个小范围联控子区域,针对域内各城市O3污染的前体物污染排放源实施统计规划、统一监测、统一监管、统一评估和统一协调的管控措施,降低O3生成率。
上述分析表明,本章提出的联动范围划分方法,既充分考虑了污染因子自身特征、各城市的经济发展水平、工业结构、城市化水平、人口规模、行政区划等社会经济因素作用,又兼顾了各地相对地理位置、自然气候条件等影响空气流域分布的的影响,克服了国内外现有区域划分方法的缺点,比仅根据污染水平表象特征、或仅考虑空气流域的影响因素、以及仅考虑行政区划因素的划分方法更科学,所划分的联动范围更精准,更有利于管理和协调,进而更有利于提高整个长三角区域联动治理的战略有效性。
撰稿人:浙江财经大学中国政府管制研究院 谢玉晶 博士
原文《Methods for defining the scopes and priorities for joint prevention and control of air pollution regions based on data-mining technologies》,作者:谢玉晶、赵来军、薛俭等,刊于《Journal of Cleaner Production》2018年第185卷